4.5 Other Relations
syntax
(define-metafunction language metafunction-contract [(name pattern ...) term metafunction-extras ...] ...)
metafunction-contract =
|
id : pattern-sequence ... -> range maybe-pre-condition maybe-post-condition maybe-pre-condition = #:pre term |
maybe-post-condition = #:post term |
range = pattern | pattern or range | pattern ∨ range | pattern ∪ range metafunction-extras = (side-condition racket-expression) | (side-condition/hidden racket-expression) | (where pat term) | (where/hidden pat term) | (where/error pat term) |
(judgment-holds (judgment-form-id pat/term ...)) |
(judgment-holds (relation-id term ...)) | (clause-name name) | or term
The contract, if present, is matched against every input to the metafunction and, if the match fails, an exception is raised. If a metavariable is repeated in a contract, it does not require the terms to be equal, unless there is an underscore subscript (i.e., the binding works like it does in define-language, not how it works in the patterns in the left-hand sides of the metafunction clauses).
If present, the term inside the maybe-pre-condition is evaluated after a successful match to the input pattern in the contract (with any variables from the input contract bound). If it returns #f, then the input contract is considered to not have matched and an error is also raised. When a metafunction returns, the expression in the maybe-post-condition is evaluated (if present), with any variables from the input or output contract bound.
The side-condition, hidden-side-condition, where, where/hidden, and where/error clauses behave as in the reduction-relation form.
The resulting metafunction raises an exception recognized by exn:fail:redex? if no clauses match or if one of the clauses matches multiple ways (and that leads to different results for the different matches).
The side-condition extra is evaluated after a successful match to the corresponding argument pattern. If it returns #f, the clause is considered not to have matched, and the next one is tried. The side-condition/hidden extra behaves the same, but is not typeset.
The where and where/hidden extra are like side-condition and side-condition/hidden, except the match guards the clause. The where/error extra is like where, except that the pattern must match.
The judgment-holds clause is like side-condition and where, except the given judgment or relation must hold for the clause to be taken.
The clause-name is used only when typesetting. See metafunction-cases.
The or clause is used to define piecewise conditional metafunctions. In particular, if any of the where or side-condition clauses fail, then evaluation continues after an or clause, treating the term that follows as the result (subject to any subsequent where clauses or side-conditions. This construction is equivalent to simply duplicating the left-hand side of the clause, once for each or expression, but signals to the typesetting library to use a large left curly brace to group the conditions in the or.
For example, here are two equivalent definitions of a biggest metafunction that typeset differently:
> (define-metafunction lc-lang biggest : natural natural -> natural [(biggest natural_1 natural_2) natural_2 (side-condition (< (term natural_1) (term natural_2)))] [(biggest natural_1 natural_2) natural_1]) > (render-metafunction biggest)
> (define-metafunction lc-lang biggest : natural natural -> natural [(biggest natural_1 natural_2) natural_2 (side-condition (< (term natural_1) (term natural_2))) or natural_1]) > (render-metafunction biggest)
Note that metafunctions are assumed to always return the same results for the same inputs, and their results are cached, unless caching-enabled? is set to #f. Accordingly, if a metafunction is called with the same inputs twice, then its body is only evaluated a single time.
As an example, these metafunctions finds the free variables in an expression in the lc-lang above:
(define-metafunction lc-lang free-vars : e -> (x ...) [(free-vars (e_1 e_2 ...)) (∪ (free-vars e_1) (free-vars e_2) ...)] [(free-vars x) (x)] [(free-vars (λ (x ...) e)) (- (free-vars e) (x ...))])
The first argument to define-metafunction is the grammar (defined above). Following that are three cases, one for each variation of expressions (e in lc-lang). The free variables of an application are the free variables of each of the subterms; the free variables of a variable is just the variable itself, and the free variables of a λ expression are the free variables of the body, minus the bound parameters.
Here are the helper metafunctions used above.
(define-metafunction lc-lang ∪ : (x ...) ... -> (x ...) [(∪ (x_1 ...) (x_2 ...) (x_3 ...) ...) (∪ (x_1 ... x_2 ...) (x_3 ...) ...)] [(∪ (x_1 ...)) (x_1 ...)] [(∪) ()]) (define-metafunction lc-lang - : (x ...) (x ...) -> (x ...) [(- (x ...) ()) (x ...)] [(- (x_1 ... x_2 x_3 ...) (x_2 x_4 ...)) (- (x_1 ... x_3 ...) (x_2 x_4 ...)) (side-condition (not (memq (term x_2) (term (x_3 ...)))))] [(- (x_1 ...) (x_2 x_3 ...)) (- (x_1 ...) (x_3 ...))])
Note the side-condition in the second case of -. It ensures that there is a unique match for that case. Without it, (term (- (x x) x)) would lead to an ambiguous match.
Changed in version 1.4 of package redex-lib: Added #:post conditions.
Changed in version 1.5: Added or clauses.
syntax
(define-metafunction/extension f language metafunction-contract [(g pattern ...) term metafunction-extras ...] ...)
For example, define-metafunction/extension may be used to extend the free-vars function above to the forms introduced by the language lc-num-lang.
(define-metafunction/extension free-vars lc-num-lang free-vars-num : e -> (x ...) [(free-vars-num number) ()] [(free-vars-num (+ e_1 e_2)) (∪ (free-vars-num e_1) (free-vars-num e_2))])
syntax
(in-domain? (metafunction-name term ...))
syntax
(define-judgment-form language mode-spec contract-spec invariant-spec rule rule ...)
mode-spec =
| #:mode (form-id pos-use ...) contract-spec =
| #:contract (form-id pattern-sequence ...) invariant-spec =
| #:inv term pos-use = I | O rule =
[premise ... dashes rule-name conclusion] |
[conclusion premise ... rule-name] conclusion = (form-id pat/term ...) premise = (judgment-form-id pat/term ...) maybe-ellipsis | (relation-id pat/term ...) maybe-ellipsis | (where pattern term) | (where/hidden pattern term) | (where/error pattern term) | (side-condition term) | (side-condition/hidden term) rule-name =
| string | non-ellipsis-non-dashes-var pat/term = pattern | term maybe-ellipsis =
| ... dashes = --- | ---- | ----- | etc.
If a mode-spec appears, each rule must be such that its premises can be evaluated left-to-right without “guessing” values for any of their pattern variables. Redex checks this property using mode-spec declaration, which partitions positions into inputs I and outputs O. Output positions in conclusions and input positions in premises must be terms; input positions in conclusions and output positions in premises must be patterns. The rule-names are used by build-derivations and by render-judgment-form.
If a mode-spec is not present, Redex cannot compute a derivation for the judgment form, instead it can check that a given derivation is valid according to the rules.
When the optional contract-spec declaration is present, Redex dynamically checks that the terms flowing through these positions match the provided patterns, raising an exception recognized by exn:fail:redex? if not. The term in the optional invariant-spec is evaluated after the output positions have been computed and the contract has matched successfully, with variables (that have underscores) from the contract bound; a result of #f is considered to be a contract violation and an exception is raised.
> (define-language nats (n ::= z (s n)))
> (define-judgment-form nats #:mode (sum I I O) #:contract (sum n n n) [----------- "zero" (sum z n n)] [(sum n_1 n_2 n_3) ------------------------- "add1" (sum (s n_1) n_2 (s n_3))])
> (judgment-holds (sum (s (s z)) (s z) (s (s (s z))))) #t
> (judgment-holds (sum (s (s z)) (s z) (s (s (s n))))) #t
> (judgment-holds (sum (s (s z)) (s z) (s (s (s (s n)))))) #f
> (judgment-holds (sum (s (s z)) (s z) (s (s (s n)))) n) '(z)
> (judgment-holds (sum (s (s z)) (s z) (s (s (s (s n))))) n) '()
> (judgment-holds (sum (s (s z)) (s z) (s (s (s n)))) (s n)) '((s z))
> (define-judgment-form nats #:mode (sumr O O I) #:contract (sumr n n n) [------------ "z" (sumr z n n)] [(sumr n_1 n_2 n_3) -------------------------- "s" (sumr (s n_1) n_2 (s n_3))]) > (judgment-holds (sumr n_1 n_2 (s (s z))) (n_1 n_2)) '(((s (s z)) z) ((s z) (s z)) (z (s (s z))))
> (define-extended-language nat-exprs nats (e ::= (+ e e) n))
> (define-judgment-form nat-exprs #:contract (same-exp e e) [(sum n_1 n_2 n_3) -------------------------- "add" (same-exp (+ n_1 n_2) n_3)] [-------------- "refl" (same-exp e e)] [(same-exp e_1 e_2) (same-exp e_2 e_3) ------------------ "trans" (same-exp e_1 e_3)] [(same-exp e_2 e_1) ------------------ "sym" (same-exp e_1 e_2)] [(same-exp e_1 e_2) ---------------------------------- "compat-l" (same-exp (+ e_1 e_3) (+ e_2 e_3))] [(same-exp e_1 e_2) ---------------------------------- "compat-r" (same-exp (+ e_3 e_1) (+ e_3 e_2))])
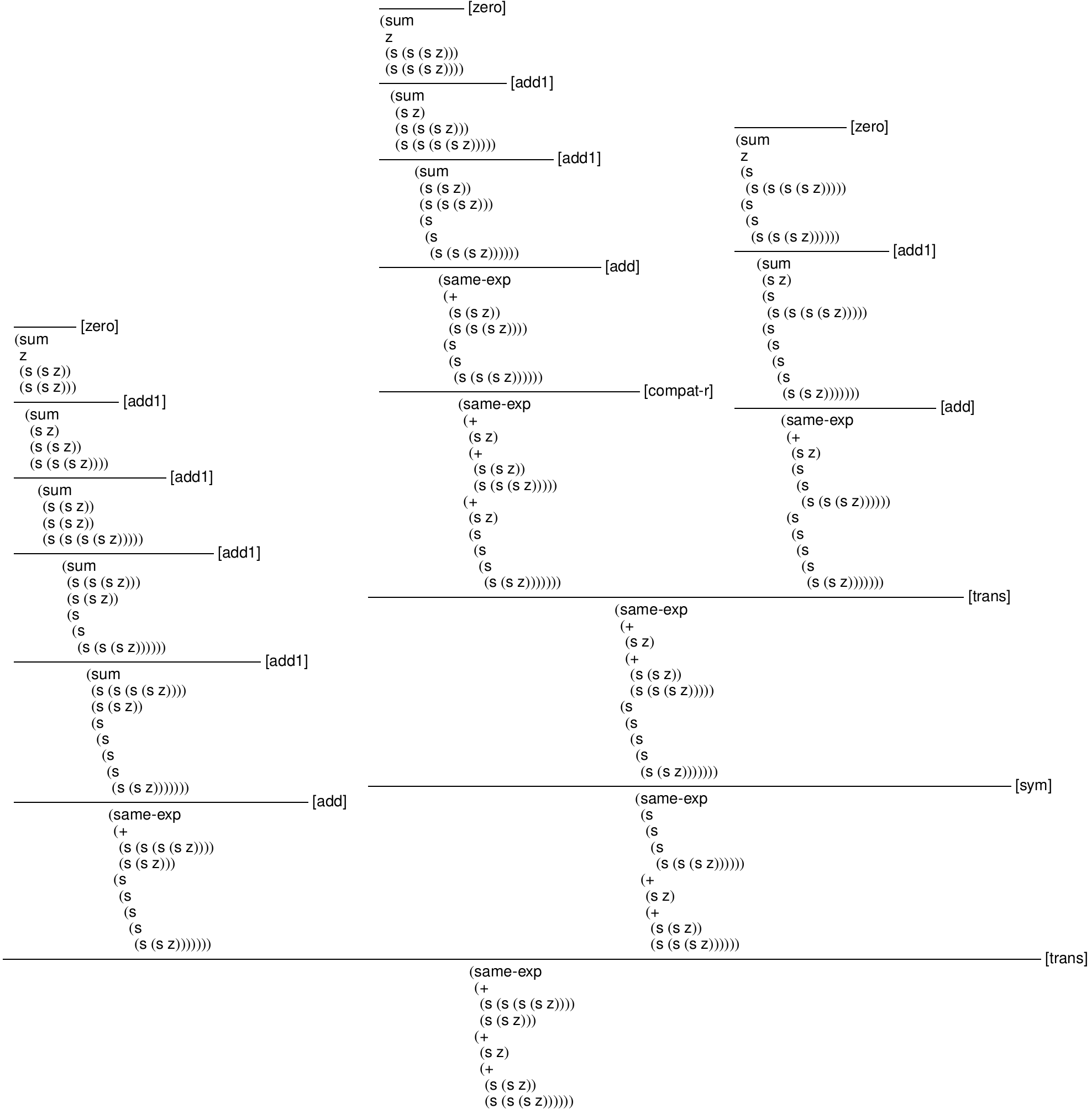
> (define same-exp-derivation (let* ([one `(s z)] [two `(s ,one)] [three `(s ,two)] [four `(s ,three)] [five `(s ,four)] [six `(s ,five)]) (derivation `(same-exp (+ ,four ,two) (+ ,one (+ ,two ,three))) "trans" (list (derivation `(same-exp (+ ,four ,two) ,six) "add" (list (car (build-derivations (sum ,four ,two n))))) (derivation `(same-exp ,six (+ ,one (+ ,two ,three))) "sym" (list (derivation `(same-exp (+ ,one (+ ,two ,three)) ,six) "trans" (list (derivation `(same-exp (+ ,one (+ ,two ,three)) (+ ,one ,five)) "compat-r" (list (derivation `(same-exp (+ ,two ,three) ,five) "add" (list (car (build-derivations (sum ,two ,three n))))))) (derivation `(same-exp (+ ,one ,five) ,six) "add" (list (car (build-derivations (sum ,one ,five n)))))))))))))
> (parameterize ([pretty-print-columns 20]) (derivation->pict nat-exprs same-exp-derivation))
> (judgment-holds same-exp same-exp-derivation) #t
The premises must be in the same order in the derivation struct’s subs field as they appear in the definition of the judgment form.
> (define-judgment-form nats #:mode (le I I) #:contract (le n n) [-------- (le z n)] [(le n_1 n_2) -------------------- (le (s n_1) (s n_2))])
> (define-metafunction nats pred : n -> n or #f [(pred z) #f] [(pred (s n)) n])
> (define-judgment-form nats #:mode (gt I I) #:contract (gt n n) [(where n_3 (pred n_1)) (le n_2 n_3) ---------------------- (gt n_1 n_2)]) > (judgment-holds (gt (s (s z)) (s z))) #t
> (judgment-holds (gt (s z) (s z))) #f
A rule’s side-condition and side-condition/hidden premises are similar to those in reduction-relation and define-metafunction, except that they do not implicitly unquote their right-hand sides. In other words, a premise of the form (side-condition term) is close to the premise (where #t term), except it does not typeset with the “#t = ”, as that would and it holds whenever the expression evaluates to any non #f value (not just #t).
> (define-judgment-form nats #:mode (even I) #:contract (even n) [-------- "evenz" (even z)] [(even n) ---------------- "even2" (even (s (s n)))])
> (define-judgment-form nats #:mode (all-even I) #:contract (all-even (n ...)) [(even n) ... ------------------ (all-even (n ...))]) > (judgment-holds (all-even (z (s (s z)) z))) #t
> (judgment-holds (all-even (z (s (s z)) (s z)))) #f
> (define-language vertices (v a b c))
> (define-judgment-form vertices #:mode (edge I O) #:contract (edge v v) [(edge a b)] [(edge b c)])
> (define-judgment-form vertices #:mode (path I I) #:contract (path v v) [---------- (path v v)] [(path v_2 v_1) -------------- (path v_1 v_2)] [(edge v_1 v_2) (path v_2 v_3) -------------- (path v_1 v_3)])
> (judgment-holds (path a c))
"typing-rules.rkt" —
defines a type system in a way that supports mechanized typesetting. When a typing judgment form can be given a mode, it can also be encoded as a metafunction using where clauses as premises, but Redex cannot typeset that encoding as inference rules. "sos.rkt" —
defines an SOS-style semantics in a way that supports mechanized typesetting. "multi-val.rkt" —
defines a judgment form that serves as a multi-valued metafunction.
(collection-file-path «filename.rkt» "redex" "examples" "define-judgment-form")
Note that current-traced-metafunctions also traces judgment forms and is helpful when debugging.
syntax
(define-extended-judgment-form language judgment-form-id mode-spec contract-spec invariant-spec rule ...)
The mode specification in this judgment form and the original must be the same.
syntax
(define-overriding-judgment-form language judgment-form-id mode-spec contract-spec invariant-spec rule ...)
The mode-spec, contract-spec, invariant-spec, and rules are as in define-judgment-form.
The mode specification in this judgment form and the original must be the same.
syntax
(judgment-holds judgment-or-relation)
(judgment-holds judgment-or-relation term) (judgment-holds judgment-form-id derivation-expr)
judgment-or-relation = (judgment-form-id pat/term ...) | (relation-id pat/term ...)
In its second form, produces a list of terms by instantiating the supplied term template with each satisfying assignment of pattern variables. In the second case, if a relation is supplied, there are no pattern variables, so the result is either a list with one element or the empty list.
In both of the first two forms, any given judgment form must have a mode.
In its third form, the judgment-form-id must not have a mode, and the derivation-expr must produce a derviation struct. The result of judgment-holds is #t when the derivation is valid, according to the rules of the judgment form, and #f otherwise. Note that the premises of the derivation must appear in the same order as the premises in the definition of the judgment form.
> (judgment-holds (sum (s (s z)) (s z) n)) #t
> (judgment-holds (sum (s (s z)) (s z) n) n) '((s (s (s z))))
procedure
(judgment-form->rule-names r) → (listof symbol?)
r : judgment-form?
syntax
(build-derivations judgment-or-relation)
> (build-derivations (even (s (s z))))
(list
(derivation
'(even (s (s z)))
"even2"
(list (derivation '(even z) "evenz" '()))))
struct
(struct derivation (term name subs) #:extra-constructor-name make-derivation) term : any/c name : (or/c string? #f) subs : (listof derivation?)
The term field holds an s-expression based rendering of the conclusion of the derivation, the name field holds the name of the clause with term as the conclusion, and subs contains the sub-derivations.
See also build-derivations.
syntax
syntax
syntax
(define-relation language relation-contract [(name pattern ...) term ... metafunction-extras ...] ...)
relation-contract =
| form-id ⊂ pattern x ... x pattern | form-id ⊆ pattern × ... × pattern
The contract specification for a relation restricts the patterns that can be used as input to a relation. For each argument to the relation, there should be a single pattern, using x or × to separate the argument contracts.
> (define-language types ((τ σ) int num (τ → τ)))
> (define-relation types subtype ⊆ τ × τ [(subtype int num)] [(subtype (τ_1 → τ_2) (σ_1 → σ_2)) (subtype σ_1 τ_1) (subtype τ_2 σ_2)] [(subtype τ τ)]) > (judgment-holds (subtype int num)) #t
> (judgment-holds (subtype (int → int) (num → num))) #f
> (judgment-holds (subtype (num → int) (num → num))) #t
procedure
(judgment-form? v) → boolean?
v : any/c
procedure
(IO-judgment-form? v) → boolean?
v : any/c
parameter
(current-traced-metafunctions) → (or/c 'all (listof symbol?))
(current-traced-metafunctions traced-metafunctions) → void? traced-metafunctions : (or/c 'all (listof symbol?))
The tracing looks just like the tracing done by the racket/trace library, except that the first column printed by each traced call indicate if this call to the metafunction is cached. Specifically, a c is printed in the first column if the result is just returned from the cache and a space is printed if the metafunction or judgment call is actually performed.
Defaults to '().
> (define-judgment-form nats #:mode (odd I) #:contract (odd n) [-------- "oddsz" (odd (s z))] [(odd n) ---------------- "odd2" (odd (s (s n)))])
> (parameterize ([current-traced-metafunctions '(odd)]) (judgment-holds (odd (s (s (s z))))))
>(odd (s (s (s z))))
> (odd (s z))
< ((odd (s z)))
<((odd (s (s (s z)))))
#t
> (parameterize ([current-traced-metafunctions '(odd)]) (judgment-holds (odd (s (s (s (s (s z))))))))
>(odd (s (s (s (s (s z))))))
c> (odd (s (s (s z))))
< ((odd (s (s (s z)))))
<((odd (s (s (s (s (s z)))))))
#t