7 Plot Utilities

8.14.900

7 Plot Utilities🔗ℹ

7.1 Formatting🔗ℹ

procedure
(digits-for-range x-min
x-max
[ base
extra-digits]) → exact-integer?
  x-min : real?
  x-max : real?
  base : (and/c exact-integer? (>=/c 2)) = 10
  extra-digits : exact-integer? = 3

Given a range, returns the number of decimal places necessary to distinguish numbers in the range. This may return negative numbers for large ranges.

Examples:

> (digits-for-range 0.01 0.02)
5
> (digits-for-range 0 100000)
-2

procedure
(real->plot-label x digits [scientific?]) → string?
  x : real?
  digits : exact-integer?
  scientific? : boolean? = #t

Converts a real number to a plot label. Used to format axis tick labels, point-labels, and numbers in legend entries.

Examples:

> (let ([d (digits-for-range 0.01 0.03)])
(real->plot-label 0.02555555 d))
".02556"
> (real->plot-label 2352343 -2)
"2352300"
> (real->plot-label 1000000000.0 4)
"1×10⁹"
> (real->plot-label 1000000000.1234 4)
"(1×10⁹)+.1234"

procedure
(ivl->plot-label i [extra-digits]) → string?
i : ivl?
extra-digits : exact-integer? = 3

Converts an interval to a plot label.

If i = (ivl x-min x-max), the number of digits used is (digits-for-range x-min x-max 10 extra-digits) when both endpoints are rational?. Otherwise, it is unspecified—but will probably remain 15.

Examples:

> (ivl->plot-label (ivl -10.52312 10.99232))
"[-10.52,10.99]"
> (ivl->plot-label (ivl -inf.0 pi))
"[-inf.0,3.141592653589793]"

procedure
(->plot-label a [digits]) → string?
a : any/c
digits : exact-integer? = 7

Converts a Racket value to a label. Used by discrete-histogram and discrete-histogram3d.

procedure
(real->string/trunc x e) → string?
x : real?
e : exact-integer?

Like real->decimal-string, but removes any trailing zeros and any trailing decimal point.

procedure
(real->decimal-string* x
min-digits
[ max-digits]) → string?
  x : real?
  min-digits : exact-nonnegative-integer?
  max-digits : exact-nonnegative-integer? = min-digits

Like real->decimal-string, but accepts both a maximum and minimum number of digits.

Examples:

> (real->decimal-string* 1 5 10)
"1.00000"
> (real->decimal-string* 1.123456 5 10)
"1.123456"
> (real->decimal-string* 1.123456789123456 5 10)
"1.1234567891"

Applying (real->decimal-string* x min-digits) yields the same value as (real->decimal-string x min-digits).

procedure
(integer->superscript x) → string?
x : exact-integer?

Converts an integer into a string of superscript Unicode characters.

Example:

> (integer->superscript -1234567890)
"⁻¹²³⁴⁵⁶⁷⁸⁹⁰"

Systems running some out-of-date versions of Windows XP have difficulty with Unicode superscripts for 4 and up. Because integer->superscript is used by every number formatting function to format exponents, if you have such a system, Plot will apparently not format all numbers with exponents correctly (until you update it).

7.2 Sampling🔗ℹ

procedure
(linear-seq start
end
num
[ #:start? start?
#:end? end?]) → (listof real?)
  start : real?
  end : real?
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Returns a list of uniformly spaced real numbers between start and end. If start? is #t, the list includes start. If end? is #t, the list includes end.

This function is used internally to generate sample points.

Examples:

> (linear-seq 0 1 5)
'(0 1/4 1/2 3/4 1)
> (linear-seq 0 1 5 #:start? #f)
'(1/9 1/3 5/9 7/9 1)
> (linear-seq 0 1 5 #:end? #f)
'(0 2/9 4/9 2/3 8/9)
> (linear-seq 0 1 5 #:start? #f #:end? #f)
'(1/10 3/10 1/2 7/10 9/10)
> (define xs (linear-seq -1 1 11))
> (plot (lines (map vector xs (map sqr xs))))

procedure
(linear-seq* points
num
[ #:start? start?
#:end? end?]) → (listof real?)
  points : (listof real?)
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Like linear-seq, but accepts a list of reals instead of a start and end. The #:start? and #:end? keyword arguments work as in linear-seq. This function does not guarantee that each inner value will be in the returned list.

Examples:

> (linear-seq* '(0 1 2) 5)
'(0 1/2 1 3/2 2)
> (linear-seq* '(0 1 2) 6)
'(0 2/5 4/5 6/5 8/5 2)
> (linear-seq* '(0 1 0) 5)
'(0 1/2 1 1/2 0)

procedure
(nonlinear-seq start
end
num
transform
[ #:start? start?
#:end? end?]) → (listof real?)
  start : real?
  end : real?
  num : exact-nonnegative-integer?
  transform : axis-transform/c
  start? : boolean? = #t
  end? : boolean? = #t

Generates a list of reals that, if transformed using transform, would be uniformly spaced. This is used to generate samples for transformed axes.

Examples:

> (linear-seq 1 10 4)
'(1 4 7 10)
> (nonlinear-seq 1 10 4 log-transform)
'(1.0 2.154434690031884 4.641588833612779 10.000000000000002)
> (parameterize ([plot-x-transform log-transform])
(plot (area-histogram sqr (nonlinear-seq 1 10 4 log-transform))))

procedure
(kde xs h [ws]) →
(-> real? real?)
(or/c rational? #f)
(or/c rational? #f)
  xs : (listof real?)
  h : (>/c 0)
  ws : (or/c (listof (>=/c 0)) #f) = #f

Given optionally weighted samples and a kernel bandwidth, returns a function representing a kernel density estimate, and bounds, outside of which the density estimate is zero. Used by density.

procedure
(silverman-bandwidth xs) → real?
xs : (listof real?)

Returns the Silverman Bandwidth estimator for the given samples. This is used as the default bandwidth by the violin renderer. See the kernel density estimation Wikipedia article for more details.

Added in version 8.5 of package plot-lib.

7.3 Plot Colors and Styles🔗ℹ

procedure
(color-seq c1
c2
num
[ #:start? start?
#:end? end?])
→ (listof (list/c real? real? real?))
  c1 : color/c
  c2 : color/c
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Interpolates between colors—red, green and blue components separately—using linear-seq. The #:start? and #:end? keyword arguments work as in linear-seq.

Example:

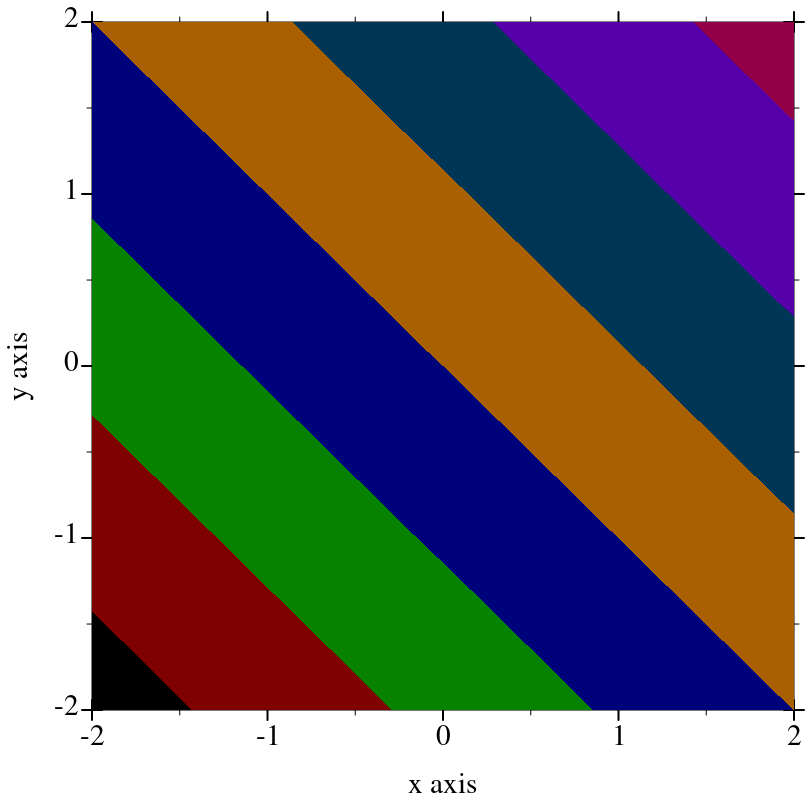
> (plot (contour-intervals (λ (x y) (+ x y)) -2 2 -2 2
#:levels 4 #:contour-styles '(transparent)
#:colors (color-seq "red" "blue" 5)))

procedure
(color-seq* colors
num
[ #:start? start?
#:end? end?])
→ (listof (list/c real? real? real?))
  colors : (listof color/c)
  num : exact-nonnegative-integer?
  start? : boolean? = #t
  end? : boolean? = #t

Interpolates between colors—red, green and blue components separately—using linear-seq*. The #:start? and #:end? keyword arguments work as in linear-seq.

Example:

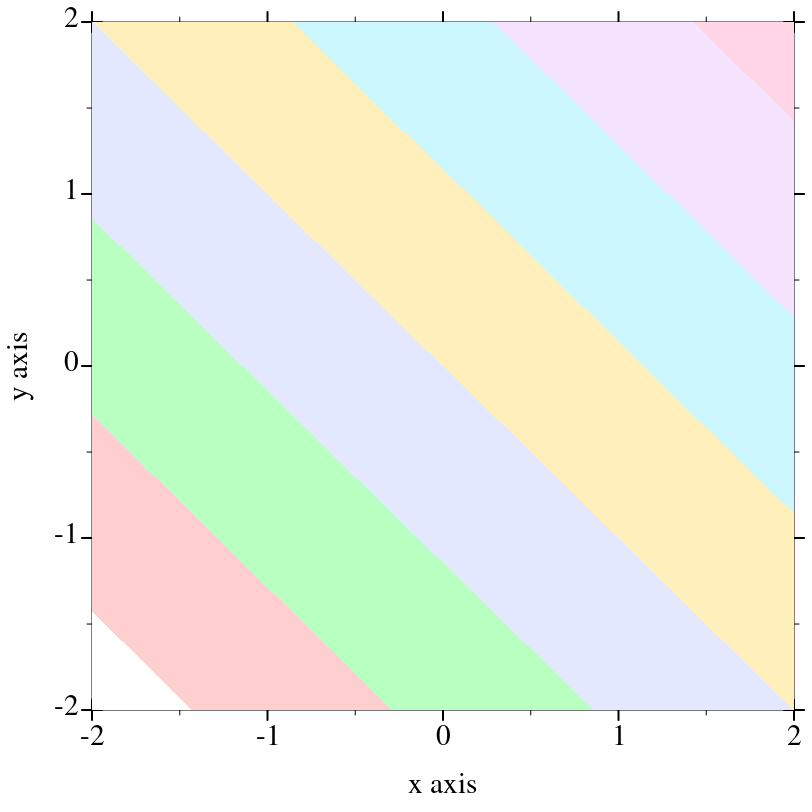
> (plot (contour-intervals (λ (x y) (+ x y)) -2 2 -2 2
#:levels 4 #:contour-styles '(transparent)
#:colors (color-seq* '(red white blue) 5)))

procedure
(->color c) → (list/c real? real? real?)
c : color/c

Converts a non-integer plot color to an RGB triplet.

Symbols are converted to strings, and strings are looked up in a color-database<%>. Lists are unchanged, and color% objects are converted straightforwardly.

Examples:

> (->color 'navy)
'(36 36 140)
> (->color "navy")
'(36 36 140)
> (->color '(36 36 140))
'(36 36 140)
> (->color (make-object color% 36 36 140))
'(36 36 140)

This function does not convert integers to RGB triplets, because there is no way for it to know whether the color will be used for a pen or for a brush. Use ->pen-color and ->brush-color to convert integers.

procedure
(->pen-color c) → (list/c real? real? real?)
c : plot-color/c

Convert a line color to an RGB triplet. Integer colors are looked up in the current plot-pen-color-map, and non-integer colors are converted using ->color. When the integer color is larger than the number of colors in the color map, it will wrap around.

Examples:

> (equal? (->pen-color 0) (->pen-color 8))
#f
> (plot (contour-intervals
         (λ (x y) (+ x y)) -2 2 -2 2
         #:levels 7 #:contour-styles '(transparent)
         #:colors (map ->pen-color (build-list 8 values))))

The example above is using the internal color map, with plot-pen-color-map set to #f.

procedure
(->brush-color c) → (list/c real? real? real?)
c : plot-color/c

Convert a fill color to an RGB triplet. Integer colors are looked up in the current plot-brush-color-map and non-integer colors are converted using ->color. When the integer color is larger than the number of colors in the color map, it will wrap around.

Examples:

> (equal? (->brush-color 0) (->brush-color 8))
#f
> (plot (contour-intervals
         (λ (x y) (+ x y)) -2 2 -2 2
         #:levels 7 #:contour-styles '(transparent)
         #:colors (map ->brush-color (build-list 8 values))))

The example above is using the internal color map, with plot-brush-color-map is set to #f. In this example, mapping ->brush-color over the list is actually unnecessary, because contour-intervals uses ->brush-color internally to convert fill colors.

The function-interval function generally plots areas using a fill color and lines using a line color. Both kinds of color have the default value 3. The following example reverses the default behavior; i.e it draws areas using line color 3 and lines using fill color 3:

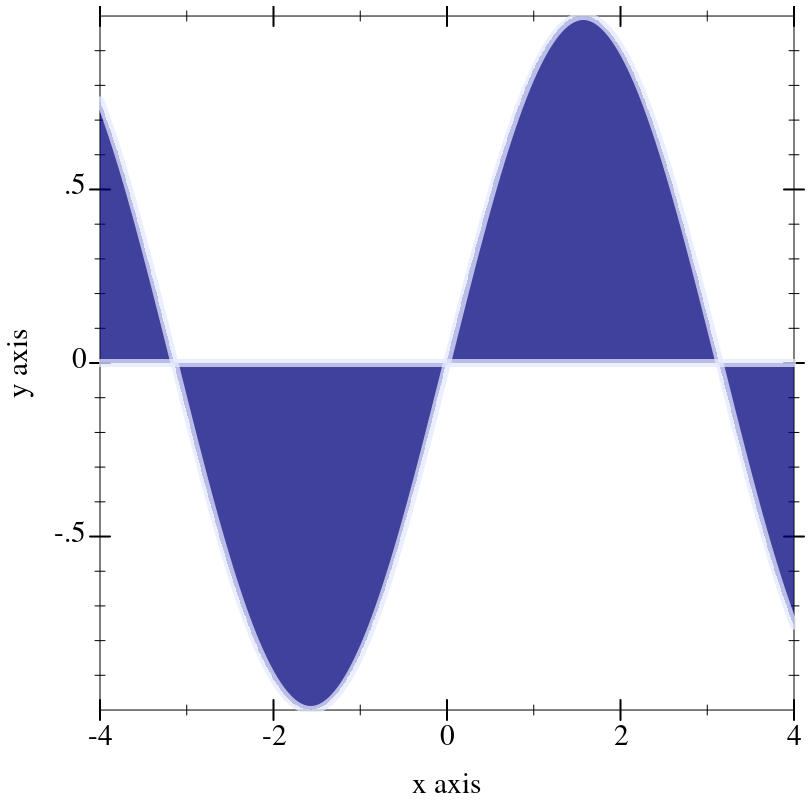
> (plot (function-interval sin (λ (x) 0) -4 4
                           #:color (->pen-color 3)
                           #:line1-color (->brush-color 3)
                           #:line2-color (->brush-color 3)
                           #:line1-width 4 #:line2-width 4))

procedure
(->pen-style s) → symbol?
s : plot-pen-style/c

Converts a symbolic pen style or a number to a symbolic pen style. Symbols are unchanged. Integer pen styles repeat starting at 5.

Examples:

> (eq? (->pen-style 0) (->pen-style 5))
#t
> (map ->pen-style '(0 1 2 3 4))
'(solid dot long-dash short-dash dot-dash)

procedure
(->brush-style s) → symbol?
s : plot-brush-style/c

Converts a symbolic brush style or a number to a symbolic brush style. Symbols are unchanged. Integer brush styles repeat starting at 7.

Examples:

> (eq? (->brush-style 0) (->brush-style 7))
#t
> (map ->brush-style '(0 1 2 3))
'(solid bdiagonal-hatch fdiagonal-hatch crossdiag-hatch)
> (map ->brush-style '(4 5 6))
'(horizontal-hatch vertical-hatch cross-hatch)

procedure
(color-map-names) → (listof symbol?)

Return the list of available color map names to be used by plot-pen-color-map and plot-brush-color-map.

Added in version 7.3 of package plot-lib.

procedure
(color-map-size name) → integer?
name : symbol?

Return the number of colors in the color map name. If name is not a valid color map name, the function will signal an error.

Added in version 7.3 of package plot-lib.

procedure
(register-color-map name color-map) → void
name : symbol?
color-map : (vectorof (list byte? byte? byte?))

Register a new color map name with the colors being a vector of RGB triplets. If a color map by that name already exists, it is replaced.

Added in version 7.3 of package plot-lib.

7.4 Plot-Specific Math🔗ℹ

7.4.1 Real Functions🔗ℹ

procedure
(polar->cartesian θ r) → (vector/c real? real?)
θ : real?
r : real?

Converts 2D polar coordinates to 2D cartesian coordinates.

procedure
(3d-polar->3d-cartesian θ ρ r) → (vector/c real? real? real?)
  θ : real?
  ρ : real?
  r : real?

Converts 3D polar coordinates to 3D cartesian coordinates. See parametric3d for an example of use.

procedure
(ceiling-log/base b x) → exact-integer?
b : (and/c exact-integer? (>=/c 2))
x : (>/c 0)

Like (ceiling (/ (log x) (log b))), but ceiling-log/base is not susceptible to floating-point error.

Examples:

> (ceiling (/ (log 100) (log 10)))
2.0
> (ceiling-log/base 10 100)
2
> (ceiling (/ (log 1/1000) (log 10)))
-2.0
> (ceiling-log/base 10 1/1000)
-3

Various number-formatting functions use this.

procedure
(floor-log/base b x) → exact-integer?
b : (and/c exact-integer? (>=/c 2))
x : (>/c 0)

Like (floor (/ (log x) (log b))), but floor-log/base is not susceptible to floating-point error.

Examples:

> (floor (/ (log 100) (log 10)))
2.0
> (floor-log/base 10 100)
2
> (floor (/ (log 1000) (log 10)))
2.0
> (floor-log/base 10 1000)
3

This is a generalization of order-of-magnitude.

procedure
(maybe-inexact->exact x) → (or/c rational? #f)
x : (or/c rational? #f)

Returns #f if x is #f; otherwise (inexact->exact x). Use this to convert interval endpoints, which may be #f, to exact numbers.

procedure
(min* r ...) → real?
r : real?
procedure
(max* r ...) → real?
r : real?

Compute the min or max of a sequence of numbers.

Examples:

> (min* 3 5 4 2 1)
1
> (max* 3 5 4 2 1)
5
> (min*)
+inf.0
> (max*)
-inf.0

7.4.2 Vector Functions🔗ℹ

procedure
(v+ v1 v2) → (vectorof real?)
  v1 : (vectorof real?)
  v2 : (vectorof real?)
procedure
(v- v1 v2) → (vectorof real?)
  v1 : (vectorof real?)
  v2 : (vectorof real?)
procedure
(vneg v) → (vectorof real?)
  v : (vectorof real?)
procedure
(v* v c) → (vectorof real?)
  v : (vectorof real?)
  c : real?
procedure
(v/ v c) → (vectorof real?)
  v : (vectorof real?)
  c : real?

Vector arithmetic. Equivalent to vector-mapp-ing arithmetic operators over vectors, but specialized so that 2- and 3-vector operations are much faster.

Examples:

> (v+ #(1 2) #(3 4))
'#(4 6)
> (v- #(1 2) #(3 4))
'#(-2 -2)
> (vneg #(1 2))
'#(-1 -2)
> (v* #(1 2 3) 2)
'#(2 4 6)
> (v/ #(1 2 3) 2)
'#(1/2 1 3/2)

procedure
(v= v1 v2) → boolean?
v1 : (vectorof real?)
v2 : (vectorof real?)

Like equal? specialized to numeric vectors, but compares elements using =.

Examples:

> (equal? #(1 2) #(1 2))
#t
> (equal? #(1 2) #(1.0 2.0))
#f
> (v= #(1 2) #(1.0 2.0))
#t

procedure
(vcross v1 v2) → (vector/c real? real? real?)
v1 : (vector/c real? real? real?)
v2 : (vector/c real? real? real?)

Returns the right-hand vector cross product of v1 and v2.

Examples:

> (vcross #(1 0 0) #(0 1 0))
'#(0 0 1)
> (vcross #(0 1 0) #(1 0 0))
'#(0 0 -1)
> (vcross #(0 0 1) #(0 0 1))
'#(0 0 0)

procedure
(vcross2 v1 v2) → real?
v1 : (vector/c real? real?)
v2 : (vector/c real? real?)

Returns the signed area of the 2D parallelogram with sides v1 and v2. Equivalent to (vector-ref (vcross (vector-append v1 #(0)) (vector-append v2 #(0))) 2) but faster.

Examples:

> (vcross2 #(1 0) #(0 1))
1
> (vcross2 #(0 1) #(1 0))
-1

procedure
(vdot v1 v2) → real?
v1 : (vectorof real?)
v2 : (vectorof real?)

Returns the dot product of v1 and v2.

procedure
(vmag^2 v) → real?
v : (vectorof real?)

Returns the squared magnitude of v. Equivalent to (vdot v v).

procedure
(vmag v) → real?
v : (vectorof real?)

Returns the magnitude of v. Equivalent to (sqrt (vmag^2 v)).

procedure
(vnormalize v) → (vectorof real?)
v : (vectorof real?)

Returns a normal vector in the same direction as v. If v is a zero vector, returns v.

Examples:

> (vnormalize #(1 1 0))
'#(0.7071067811865475 0.7071067811865475 0)
> (vnormalize #(1 1 1))
'#(0.5773502691896258 0.5773502691896258 0.5773502691896258)
> (vnormalize #(0 0 0.0))
'#(0 0 0.0)

procedure
(vcenter vs) → (vectorof real?)
vs : (listof (vectorof real?))

Returns the center of the smallest bounding box that contains vs.

Example:

> (vcenter '(#(1 1) #(2 2)))
'#(3/2 3/2)

procedure
(vrational? v) → boolean?
v : (vectorof real?)

Returns #t if every element of v is rational?.

Examples:

> (vrational? #(1 2))
#t
> (vrational? #(+inf.0 2))
#f
> (vrational? #(#f 1))
vrational?: contract violation
  expected: real?
  given: #f
  in: an element of
      the 1st argument of
      (-> (vectorof real?) any)
  contract from:
      <pkgs>/plot-lib/plot/private/common/math.rkt
  blaming: top-level
   (assuming the contract is correct)
  at: <pkgs>/plot-lib/plot/private/common/math.rkt:304:9

7.4.3 Intervals and Interval Functions🔗ℹ

struct
(struct ivl (min max)
    #:extra-constructor-name make-ivl)
  min : real?
  max : real?

Represents a closed interval.

An interval with two real-valued endpoints always contains the endpoints in order:

> (ivl 0 1)
(ivl 0 1)
> (ivl 1 0)
(ivl 0 1)

An interval can have infinite endpoints:

> (ivl -inf.0 0)
(ivl -inf.0 0)
> (ivl 0 +inf.0)
(ivl 0 +inf.0)
> (ivl -inf.0 +inf.0)
(ivl -inf.0 +inf.0)

Functions that return rectangle renderers, such as rectangles and discrete-histogram3d, accept vectors of ivls as arguments. The ivl struct type is also provided by plot so users of such renderers do not have to require plot/utils.

procedure
(rational-ivl? i) → boolean?
i : any/c

Returns #t if i is an interval and each of its endpoints is rational?.

Example:

> (map rational-ivl? (list (ivl -1 1) (ivl -inf.0 2) 'bob))
'(#t #f #f)

procedure
(bounds->intervals xs) → (listof ivl?)
xs : (listof real?)

Given a list of points, returns intervals between each pair.

Use this to construct inputs for rectangles and rectangles3d.

Example:

> (bounds->intervals (linear-seq 0 1 5))
(list (ivl 0 1/4) (ivl 1/4 1/2) (ivl 1/2 3/4) (ivl 3/4 1))

procedure
(clamp-real x i) → real?
x : real?
i : ivl?

7.5 Dates and Times🔗ℹ

procedure
(datetime->real x) → real?
x : (or/c plot-time? date? date*? sql-date? sql-time? sql-timestamp?)

Converts various date/time representations into UTC seconds, respecting time zone offsets.

For dates, the value returned is the number of seconds since a system-dependent UTC epoch. See date-ticks for more information.

To plot a time series using dates pulled from an SQL database, simply set the relevant axis ticks (probably plot-x-ticks) to date-ticks, and convert the dates to seconds using datetime->real before passing them to lines. To keep time zone offsets from influencing the plot, set them to 0 first.

struct
(struct plot-time (second minute hour day)
    #:extra-constructor-name make-plot-time)
  second : (and/c (>=/c 0) (</c 60))
  minute : (integer-in 0 59)
  hour : (integer-in 0 23)
  day : exact-integer?

A time representation that accounts for days, negative times (using negative days), and fractional seconds.

Plot (specifically time-ticks) uses plot-time internally to format times, but because renderer-producing functions require only real values, user code should not need it. It is provided just in case.

procedure
(plot-time->seconds t) → real?
t : plot-time?
procedure
(seconds->plot-time s) → plot-time?
s : real?

Convert plot-times to real seconds, and vice-versa.

Examples:

> (define (plot-time+ t1 t2)
    (seconds->plot-time (+ (plot-time->seconds t1)
                           (plot-time->seconds t2))))
> (plot-time+ (plot-time 32 0 12 1)
              (plot-time 32 0 14 1))
(plot-time 4 1 2 3)

7.6 Plot Metrics🔗ℹ

interface
plot-metrics<%> : interface?

The plot-metrics<%> interface allows obtaining plot area positions on the plots returned by plot, plot-snip, plot-bitmap, plot/dc, as well as their 3D variants, plot3d, plot3d-snip, plot3d-bitmap and plot3d/dc. All plot objects returned by these functions implement this interface.

For plots created by plot-pict and plot3d-pict, there is a separate set of functions that provide the same functionality, for example, see plot-pict-bounds.

method
(send a-plot-metrics get-plot-bounds)
→ (vectorof (vector/c real? real?))
Return the bounds of the plot as a vector of minimum and maximum values, one for each axis in the plot. For 2D plots, this method returns a vector of two elements, for the X and Y axes, while 3D plots return a vector of three elements for the X, Y and Z axes.
The values returned are in plot coordinates, to obtain the coordinates on the drawing surface (i.e. image coordinates), use plot->dc on these bounds.
Plot bounds for interactive plots, like those produced by plot and plot-snip, can change as the user zoom in and out the plot, get-plot-bounds always returns the current bounds of the plot, but they might be invalidated by a user operation.
method
(send a-plot-metrics plot->dc coordinates) → (vectorof real?)
coordinates : (vectorof real?)
Convert coordinates from plot coordinate system to the drawing coordinate system (that is, image coordinates). For 2D plots, coordinates is a vector of two values, the X and Y coordinates on the plot, while for 3D plots it is a vector of three values, the X, Y and Z coordinates.
This method can be used, for example, to determine the actual location on the image where the coordinates 0, 0 are. It can also be used to determine the location of the plot area inside the image, by calling it on the plot bounds returned by get-plot-bounds.
For interactive plots, the coordinates might change as the user zooms in and out the plot.
method
(send a-plot-metrics dc->plot coordinates) → (vectorof real?)
coordinates : (vectorof real?)
For 2D plots, this method returns the 2D plot coordinates that correspond to the input coordinates, which are in the draw context coordinate system.
For 3D plots, this method returns a 3D position on the plane perpendicular to the user view for the plot. Together with the normal vector for this plane, returned by plane-vector, the projection line can be reconstructed.
This is the reverse operation from plot->dc and same remark about the user zooming in and out the plot applies.
method
(send a-plot-metrics plane-vector) → (vectorof real?)
Return the unit vector representing the normal of the screen through the plot origin. For 2D plots this always returns #(0 0 1), for 3D plots this unit vector can be used to reconstruct plot coordinates from draw context coordinates.
For interactive 3D plots, the returned value will change if the user rotates the plot.
Added in version 8.1 of package plot-lib.

procedure
(plot-pict? any) → boolean?
any : any/c

Return #t if any is a plot returned by plot-pict. This can be used to determine if the functions plot-pict-bounds, plot-pict-plot->dc, plot-pict-dc->plot and plot-pict-plane-vector can be called on it.